Les Cahiers Rationalistes N°658 janvier-février 2019
À propos de prévisions
On lira ici le texte profondément remanié et complété par l’auteur d’un exposé oral présenté lors d’une réunion de la section nantaise de l’UR.
De la pythie de Delphes à nos jours, le désir ou le besoin de prévoir apparaissent comme une préoccupation constante du genre humain. Aujourd’hui, on cherche à prévoir dans les sciences de la nature : changement climatique, montée des eaux, trajectoire d’un nuage volcanique, etc., aussi bien que dans les sciences sociales : milliers de morts d’une pandémie annoncée, financement des retraites en… 2050 ou taux de croissance du PIB.
L’état actuel des sciences et des techniques permet – au moins dans certains cas – de prévoir en avançant des arguments qui peuvent être soumis à analyses et jugements critiques. Mais la diversité des méthodes mises en œuvre selon les domaines concernés invite cependant à accorder une plus ou moins grande crédibilité à telle ou telle prévision. C’est cette crédibilité qui est, indirectement, l’objet de cet exposé. On examine quelques questions de méthode en s’en tenant aux prévisions faites à partir de modèles mathématiques déterministes et qui font appel à des calculs. Il ne sera donc pas fait état des prévisions faites sans calculs, mais à partir de savoir-faire accumulé, d’expériences et de connaissances empiriques ; le pronostic médical courant, par exemple, est une prévision faite sans recourir à des calculs. Il ne sera pas fait état, non plus, de prévisions élaborées à partir de considérations statistiques ou probabilistes.
On parlera constamment de modèle. On entend par là un ensemble d’équations mathématiques dont la solution décrit l’évolution dans le temps du phénomène étudié. Les modèles sont établis à partir de grandes lois de la physique, de la chimie, etc. en faisant généralement des hypothèses simplificatrices qui doivent être soigneusement analysées. Mais là n’est pas le propos essentiel de cet exposé qui se limite à l’examen de quelques difficultés qui peuvent apparaître lors de la résolution numérique d’un modèle.
Pour simplifier, trois situations sont examinées, correspondant à ce que l’on peut appeler, sans plus de précision, la qualité du modèle, qualité qui peut varier de nulle à excellente. La plus grande partie de l’exposé est consacrée au cas général d’un modèle dont on sait qu’il comporte des éléments inconnus ou mal connus.
La diversité des situations apparaît et invite à la prudence dans nombre de cas, lorsqu’il s’agit de prévoir. Quelques formules mathématiques précisent le propos mais leur lecture peut être omise par le lecteur peu ou pas familiarisé avec cette écriture.
- ON DISPOSE D’UN MODÈLE DE BONNE QUALITÉ
Le cas le plus évident est celui de la mécanique newtonienne appliquée au calcul des trajectoires des astres. Comme les perturbations aléatoires sont inexistantes ou négligeables, il n’y a aucune difficulté théorique ou pratique pour calculer la position de la Lune le 28 avril 2020 à 0 h 35 !
Remarquons aussi que les équations de la mécanique céleste présentent cette particularité de pouvoir être résolues à rebours et qu’on peut donc remonter le temps et vérifier que le chrisme vu par Constantin dans le ciel avant sa victoire sur Maxence au pont Milvius le 28 octobre 312 correspondait à une conjonction et à un alignement sur la voûte céleste des planètes Mars, Saturne, Jupiter et Vénus. Uranus était aussi dans l’alignement ; mais il ne pouvait la voir, faute d’instrument.
Un autre exemple nous est donné par Jean-Baptiste Tavernier (1605- 1680), grand commerçant itinérant en Asie. Il relate avoir vu, à Patna en Inde, le 12 mai 1666, une éclipse du Soleil « à une heure après midi ». L’historien peut vérifier, avec un logiciel d’astronomie et après quelques clicks, que Tavernier n’a rien inventé et que lieu et date sont exacts.
Cette possibilité de résoudre à rebours n’est pas générale ; elle n’existe pas pour les systèmes dissipatifs comme les systèmes thermiques par exemple.
La mécanique céleste pourrait être considérée comme achevée et quasi parfaite avec des modèles figés et immuables, comme feignent de le croire les tenants de l’astrologie. Mais ce n’est pas le cas. Par exemple, tous les paramètres des mouvements planétaires varient plus ou moins lentement au cours du temps. C’est ainsi que l’excentricité de l’ellipse décrite par la Terre autour du Soleil, notée e, varie lentement au cours du temps. L’évaluation des formules proposées par l’IMCCE[1] donne e = 0, 0167086 le 1er janvier 2000 et e = 0,0166665 le 1er janvier 2100.
On sait aussi que la mécanique newtonienne ne donnait pas d’explication satisfaisante à l’avance du périhélie de Mercure. C’est en 1915 qu’Einstein en a donné une explication dans le cadre de la Relativité générale. C’est un bel exemple de construction du savoir scientifique où une nouvelle théorie vient compléter la précédente.
La question de la stabilité du système solaire, posée par Newton il y a 350 ans, a été étudiée par les plus grands noms de l’astronomie. Une recension de ces travaux a été faite aujourd’hui par l’astronome Jacques Lascar[2] qui apporte sa contribution à la question en montrant que, sur le long terme, les trajectoires des planètes sont de nature chaotique et que « les collisions entre planètes ou leur éjection sont possibles en moins de cinq milliards d’années », c’est-à-dire avant la fin de vie du Soleil, estimée à une dizaine de milliards d’année depuis sa création.
Un exemple de modèle de bonne qualité nous est aussi donné par la loi d’Ohm (U = R I), enseignée dès la classe de quatrième dans les collèges. Il ne saurait être question de la remettre en cause, mais un exemple simple nous montre qu’on ne peut pas toujours l’appliquer brutalement : mesurons la résistance du filament de tungstène d’une ampoule de 25 W éteinte ; un ohmmètre nous indique 219 Ω . Le calcul de la puissance P de l’ampoule alimentée par la tension du réseau (230 V) nous donne P = 2302/219 , soit environ 242 W au lieu des 25 W attendus. Erreur de calcul ? Non : on a simplement oublié que la résistance du filament dépend de la température et qu’elle n’est pas la même à la température ambiante qu’à 2000°C, température du filament en service sous 230 V.
L’énoncé de la loi d’Ohm suppose donc, sans qu’on le dise toujours explicitement, que la valeur de la résistance, R, est une constante, indépendante de la température et du courant I qui la traverse.
- IL N’Y A PAS DE MODÈLE
En l’absence de modèle aucune prévision rigoureuse basée sur un calcul n’est possible dans le cadre déterministe qui nous occupe. Mais il est des cas où, poussé par la nécessité, on peut être tenté de se donner un modèle a priori et d’effectuer des calculs.
Considérons, par exemple, l’évolution de la population de la France au fil des années. Celle-ci est représentée sur la figure 1, entre 1990 et 2015. Les données sont celles de l’INSEE ; elles correspondent au 1er janvier de chaque année.
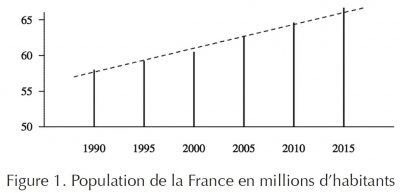
Plaçons-nous au 1er janvier 2010 et tentons de prévoir la population au 1er janvier 2015. En l’absence de modèle, on cherche à extrapoler au mieux les données existantes. Plusieurs solutions techniques sont possibles dont voici deux exemples :
Extrapolation linéaire
On calcule la droite dite des moindres carrés qui approche les cinq points connus et on la prolonge jusqu’en 2015. L’opération est souvent appelée régression linéaire. Elle est facilement réalisable avec une calculatrice de poche. Le résultat est représenté sur la figure 1 en trait interrompu. La population « prévue » pour 2015 est 66,029 au lieu des 66,694 millions d’habitants effectivement recensés. L’intérêt d’une prévision aussi peu précise est bien faible.
Extrapolation polynomiale
Elle consiste à calculer les coefficients d’un polynôme de degré quatre qui passe par les cinq points connus et à extrapoler à l’aide de ce polynôme. Le résultat est représenté sur la figure 2 par la courbe en trait interrompu. La population « prévue » pour 2015 avec ce procédé est 62,435 au lieu des 66,694 millions d’habitants effectivement recensés. Ce type d’extrapolation est manifestement à rejeter.
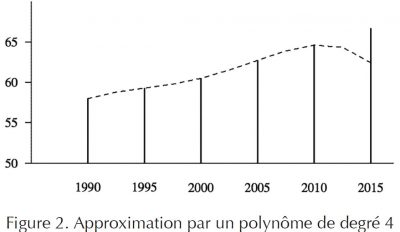
On pourrait multiplier les exemples en raffinant la technique mais toutes ces extrapolations reposent sur des idées posées a priori et non explicitées, en l’occurrence celles que les conditions qui déterminent l’évolution de la population entre 1990 et 2010 subsistent à peu près entre 2010 et 2015.
Les prévisions en matière de population sont l’objet de travaux effectués et publiés par l’INSEE. On en trouve un extrait dans le rapport n° 1619 de INSEE Première, disponible sur le site de l’organisme, sous le titre « Projections de population à l’horizon 2070 ». Les projections sont basées sur trois facteurs : la fécondité, l’espérance de vie et le solde migratoire. Six scénarios sont présentés avec, pour chaque facteur, une hypothèse haute et une hypothèse basse. Les résultats sont de 87,6 millions d’habitants en 2070 avec des hypothèses hautes et 66,1 millions avec des hypothèses basses. Un scénario central est donné : 76,4 millions d’habitants.
Une projection faite par régression linéaire avec les données des figures 1 et 2 (de 1990 à 2015) nous donne 85,7 millions d’habitants en 2070. Tous ces résultats illustrent ce que le rapport qualifie d’« incertitudes inhérentes à un tel exercice », même si « Le choix des hypothèses de projection a fait l’objet d’une large consultation d’experts ». On peut aussi ajouter que toutes ces projections ne peuvent pas prendre en compte des phénomènes imprévisibles par nature comme les pandémies, les politiques de purification ethnique, les conflits armés, etc.
3. LE CAS GÉNÉRAL
C’est celui où l’on dispose d’un ou de plusieurs modèles ; mais aussi où les phénomènes sont compliqués, où l’on n’est pas sûr de tenir compte de tous les facteurs, où les coefficients qui interviennent dans les équations ne sont pas connus avec précision, où les conditions initiales ne sont que partiellement connues, où la résolution des équations du modèle présente des difficultés, etc. En bref : le quotidien du scientifique.
Un exemple simple nous permet d’illustrer deux difficultés qui peuvent apparaître lors du calcul d’une prévision. Un autre exemple montre que la solution d’un modèle peut présenter des comportements qu’on pourrait qualifier de surprenants sans une étude préalable circonstanciée.
Partons des équations de Lorenz (Edward Norton). Elles modélisent des phénomènes climatiques qu’il est inutile de détailler ici parce qu’elles ne nous servent que de paradigme pour illustrer les effets évoqués. On trouvera des explications détaillées à leur sujet dans Wikipédia.
Ces équations s’écrivent sous la forme d’un système de trois équations différentielles non linéaires couplées où t représente le temps et où le point représente la dérivée par rapport au temps :
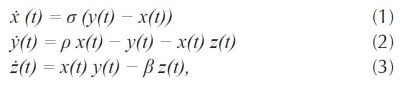
auquel on adjoint des conditions initiales à l’instant t = 0. Les trois coefficients σ, ρ et β sont des nombres réels, supposés connus. On prend ici σ = 10, ρ = 28 et β = 8/3.
Influence des conditions initiales sur la solution
Les conditions initiales du système (1-2-3) sont nécessaires à sa résolution. Il s’agit de fixer les valeurs x(0) , y(0) et z(0) des variables à l’instant initial t = 0. Celles-ci sont généralement obtenues à partir de mesures réalisées sur le processus étudié et sont inévitablement affectées d’une incertitude liée aux instruments. La question est alors de savoir quelle est l’influence de ces incertitudes de mesure sur la solution calculée par résolution des équations du modèle.
On peut faire une expérience en faisant varier légèrement une condition initiale, ici de 1%. C’est ce qu’illustre la figure 3 qui montre clairement l’influence de la condition initiale y(0) sur la solution y(t) correspondante. Les trois coefficients σ , ρ et β sont identiques pour les deux courbes.
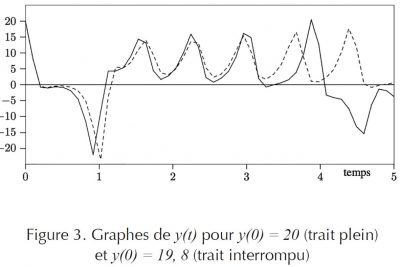
On peut aussi remarquer que la modification de la condition initiale de la variable y entraîne des modifications sur les trajectoires de x(t) et z(t), le phénomène étant dû aux couplages des équations du modèle. Les courbes correspondantes ne sont pas présentées ici.
L’exemple ci-dessus fait partie d’une classe de systèmes appelés chaotiques, au sens mathématique du terme. Cela signifie que, sans remettre en cause le déterminisme du système, il est pratiquement impossible de calculer la solution à long terme, sauf à connaître la condition initiale avec une précision parfaite. Une étude théorique peut, dans des cas pas trop compliqués, donner des indications sur l’influence de la condition initiale sur la solution. Sinon, on est contraint de procéder à de nombreux essais numériques pour évaluer cette influence, comme c’est le cas pour l’étude de la stabilité à long terme du système solaire[3].
Cette question de la sensibilité de la solution aux conditions initiales se pose de la même manière lorsqu’on passe en dimension 2 ou 3 en espace. Le système d’équations différentielles ordinaires est alors remplacé par un système d’équations aux dérivées partielles. Le phénomène est illustré par le célèbre effet papillon cité par Lorenz qui veut, de manière très exagérée, qu’un battement d’aile de papillon puisse provoquer, un peu plus tard, un ouragan à des milliers de kilomètres. Cette sensibilité de la solution aux conditions initiales est à l’origine – au moins pour une part – de la limitation à quelques jours des prévisions météorologiques.
Sensibilité de la solution aux variations des coefficients
Tout modèle mathématique d’un processus comporte des coefficients qui sont des nombres ou, dans les cas plus compliqués, des fonctions d’une ou plusieurs variables d’état. C’est ainsi que notre exemple comprend les trois coefficients σ, ρ et β qui, dans le cas d’une modélisation d’un phénomène physique, sont des nombres connus avec une plus ou moins grande incertitude, celle-ci étant liée à la précision de l’instrumentation, à la méthodologie de mesure, etc.
La question évoquée ici est celle de l’incidence de cette incertitude sur la solution du modèle. Pour illustrer le phénomène, considérons de nouveau le système (1-2-3). Des résolutions numériques permettent de tracer les graphes des trois fonctions x, y et z pour différentes valeurs des coefficients et de visualiser ainsi l’influence de chacun d’eux sur la solution. La figure 4 illustre l’influence d’une variation de l’ordre de 0, 3% de la valeur du coefficient ρ du modèle sur une des solutions, sachant que les conditions initiales sont identiques pour les deux solutions présentées.
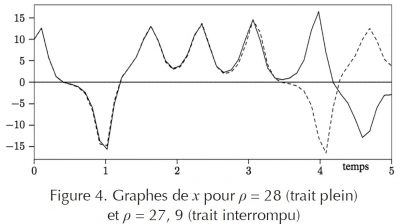
On voit que les deux solutions sont très proches l’une de l’autre jusqu’à l’instant t = 3 mais diffèrent ensuite de manière significative. On en conclut à la nécessité de connaître les valeurs des coefficients avec une précision suffisante pour que la solution soit représentative de la réalité. Mais qu’en est- il de ces valeurs des coefficients ? Si ceux-ci correspondent à des grandeurs physiques bien connues, il n’y a généralement pas de problème. C’est le cas, par exemple, de la masse volumique de l’eau à différentes températures, etc. Mais certains coefficients comme des coefficients d’échange ou de transfert ne sont pas accessibles par une mesure directe. On procède alors à leur identification. Cela signifie qu’on calcule – on ajuste – la valeur des coefficients pour que la solution du modèle soit la plus proche possible de mesures réalisées sur le phénomène étudié.
Lorsque les coefficients sont des nombres réels, comme c’est le cas dans l’exemple élémentaire cité ici, cette identification peut être relativement simple, à condition de ne pas avoir trop de coefficients à identifier simultanément et de disposer de suffisamment de données. L’affaire se complique considérablement lorsque les coefficients ne sont pas des constantes mais des fonctions inconnues d’une ou de plusieurs variables d’état, ici x, y et z .
En dehors des difficultés techniques de l’opération, une difficulté méthodologique apparaît, qu’il est utile d’évoquer brièvement. Considérons un coefficient d’échange c entre deux milieux et supposons qu’il dépende de la température θ , soit c(θ) . Pour des données obtenues à partir d’expériences réalisées avec θ compris entre 0 et 20 °C, on pourrra identifier une « bonne » fonction ĉ(θ) . Mais lorsqu’on veut produire des prévisions, qu’en est-il si la température dépasse 20 °C et qu’on est dans l’impossibilité de faire des mesures au delà de 20 °C ? Il faut alors extrapoler la fonction ĉ(θ) au delà de 20 °C et on est, d’un point de vue méthodologique, dans la situation décrite dans le paragraphe 2 ci-dessus. On peut avoir de bonnes raisons de penser que… et faire des choix. Mais une part d’arbitraire subsiste dans ceux-ci.
L’exemple présenté ci-dessus montre qu’une faible variation d’un coefficient peut entraîner une modification sensible de la solution. Mais on pourrait aussi dire que, globalement, la solution reste oscillante avec des variations bornées et que, dans une langue un peu imagée, la nature de la solution est inchangée. Il est cependant des cas où la nature même de la solution est affectée par une faible variation d’un coefficient. C’est ce qui se produit lorsqu’on a affaire à une bifurcation dont voici maintenant un exemple simple.
Considérons le système suivant, écrit en coordonnées polaires où ρ(t) est la distance au pôle à l’instant t et θ(t) l’angle polaire au même instant :
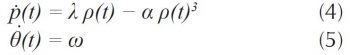
où λ est un nombre réel et où α et ω sont des nombres réels positifs.
Lorsque t tend vers l’infini, on peut établir et vérifier numériquement que la solution du système (4-5), associée à la condition initiale ρ(0) > 0, s’enroule indéfiniment dans le sens direct autour du pôle. Mais on démontre aussi qu’il existe une valeur critique λc du coefficient λ, ici λc = 0, ayant la propriété suivante : pour λ > λc, la solution tend asymptotiquement vers le cercle centré au pôle et de rayon égal à √λ/α parcouru indéfiniment et appelé cercle limite tandis que pour λ ≤ λc, la solution tend vers le pôle. C’est ce qu’illustre la figure 5 ci-dessous. La condition initiale est la même pour les courbes (a) et (b), soit ρ(0) = 0,5 et θ(0) = 0 et il en va de même pour les coefficients α et ω qui valent respectivement 0,1 et 5. La courbe (a) correspond à λ = −0,5 et la courbe (b) à λ = +0,5. Les flèches indiquent le sens du temps.
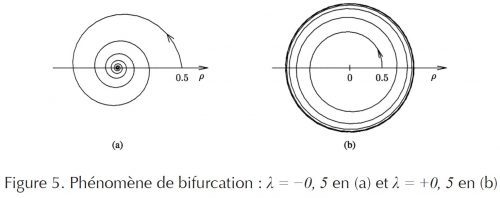
Ce phénomène de bifurcation n’est pas une simple curiosité mathématique.
On le rencontre en physique avec, par exemple, l’existence d’une masse critique d’uranium ou de plutonium pour engendrer une explosion nucléaire. En biologie, on en trouve des exemples lors de l’étude du confinement des chaînes (ou voies) métaboliques.
Avec un peu d’imagination poétique on peut, par exemple, concevoir un processus physiologique sensible à un coefficient λ et tel que pour λ supérieur à une valeur critique λc le processus décrit un cycle limite stable en assurant la pérennité de la vie alors que le processus tend vers zéro, c’est-à-dire la mort, dès que ce coefficient λ devient inférieur ou égal à λc.
4. RÉSOLUTION NUMÉRIQUE
Après avoir écrit un modèle mathématique d’un phénomène, il faut le résoudre, c’est-à-dire calculer sa solution pour être en mesure, ensuite, de prévoir à partir des données existantes. Historiquement, on a cherché et trouvé des solutions qui s’expriment à l’aide des fonctions usuelles : polynômes, fonctions trigonométriques, etc. L’opération peut être longue et difficile mais on a su calculer les trajectoires des astres à partir des lois de Kepler avant l’invention des ordinateurs !
Il n’en demeure pas moins qu’aujourd’hui, pratiquement, tous les modèles sont résolus numériquement avec des ordinateurs et que c’est avec ces mêmes ordinateurs qu’on fait des prévisions.
La fiabilité des résultats présentés doit donc aussi être examinée en s’arrêtant un instant sur ces moyens de calcul, indépendamment de la qualité supposée des modèles. Trois aspects de la question sont à évoquer qui sont, par ordre d’importance décroissante, la fiabilité du matériel, celle des logiciels et celle de la programmation.
Fiabilité des calculs liée au matériel
C’est le matériel – le processeur – qui effectue les opérations élémentaires d’arithmérique, de trigonométrie, de logique, de comparaisons, etc. Aucune erreur dans ces opérations n’étant admissible, les constructeurs livrent sur le marché des produits irréprochables de ce point de vue, ce qui fait que les ordinateurs sont réputés calculer juste et « ne pas se tromper ».
Rappelons cependant, pour l’anecdote, que le premier microprocesseur Pentium, sorti en 1994, donnait, dans quelques cas il est vrai rarissimes mais de ce fait d’autant plus dangereux, des résultats faux lors de divisions effectuées par son unité de calcul en virgule flottante. L’affaire fit suffisamment de bruit pour amener le constructeur Intel à rendre public les algorithmes numériques fondus dans le silicium.
La fiabilité des calculs liée au matériel n’est, pratiquement, jamais mise en cause aujourd’hui dans l’analyse critique de résultats scientifiques.
Fiabilité des logiciels
La résolution numérique des modèles passe par l’écriture et l’exécution de programmes écrits dans des langages comme Fortran, C++, Matlab, Scilab, etc. Ces langages font appel à des programmes ou sous- programmes externes ou internes au système informatique et dont l’ensemble constitue un logiciel. Ces programmes ou sous-programmes résolvent chacun un problème spécifique avec une méthode – un algorithme – donnée.
Les logiciels de calcul scientifique de grande diffusion font régulièrement l’objet de « mises-à-jour ». Des erreurs, parfois nombreuses sont corrigées… en attendant la prochaine révision. On pourrait donc s’inquiéter de la fiabilité de ces logiciels en assistant à ces révisions successives. En y regardant de plus près on s’aperçoit que les modifications apportées sont des améliorations relatives à l’utilisation des programmes et à la correction d’erreurs mineures – les fameux bugs – lesquels n’affectent généralement pas la validité des calculs.
Comme ces logiciels sont utilisés chaque jour par des milliers d’utilisateurs, on n’a pas de raison sérieuse de douter a priori de l’exactitude des résultats qu’ils fournissent, dans la mesure où ils sont utilisés à bon escient. Malgré ces quasi-certitudes, des erreurs peuvent subsister dans les logiciels. Citons le cas de la plate-forme offshore Sleipner qui a coulé au large de la Norvège le 23 août 1991 à la suite d’une inaccurate finite element approximation faite par le logiciel NASTAN (NAsa STructural ANalysis) lors de la conception. Ce logiciel, développé initialement par la NASA, effectue des calculs selon des méthodes d’éléments finis. Il comporte de l’ordre de un million de lignes de programmation.
Ceci nous conduit à évoquer un aspect plus délicat de la fiabilité des prévisions obtenues par résolution numérique de modèles, à savoir la programmation proprement dite.
Fiabilité de la programmation
Quiconque s’est essayé à programmer sait que les causes d’erreurs sont nombreuses. Oublions la parenthèse qui manque et le O à la place du 0, vite signalés par le compilateur et corrigés dans la foulée. Mais il existe des erreurs plus subtiles : le programme tourne mais donne des résultats invraisemblables (c’est le cas généralement le plus favorable) ou vraisemblables mais faux (c’est le cas le plus difficile).
La question est assez importante pour avoir donné lieu à la mise au point de méthodes destinées à réduire les risques d’erreurs et à apporter rigueur et lisibilité à la programmation : programmation modulaire, structurée, par objets, etc. Écrire des codes de programmation est une discipline à part entière.
Mais la principale difficulté est ailleurs : un même problème peut être résolu numériquement selon plusieurs méthodes. Les équations de Lorenz, citées plus haut, ont été résolues selon une méthode de Runge-Kutta, mais d’autres méthodes étaient possibles. Le choix d’une méthode doit prendre en compte des critères souvent contradictoires comme la précision des résultats, la rapidité des calculs, l’encombrement de la mémoire de l’ordinateur, la facilité de mise en œuvre. Des connaissances appronfondies en analyse numérique sont alors indispensables pour choisir une méthode plutôt qu’une autre, en fonctions de résultats de convergence, de formules de majorations d’erreurs, etc. On est loin de l’aspect purement technique de la programmation vue sous son seul aspect d’écriture de codes informatiques.
Quelle confiance accorder aux résultats de l’exécution d’un programme ? La réponse ne peut être qu’expérimentale. La communauté scientifique s’accorde pour considérer comme fait scientifique ce qui a été observé plusieurs fois, dans les mêmes conditions, par des observateurs indépendants. Il en est de même pour des prévisions obtenues à partir de calculs. Elles n’ont de crédibilité que si des résultats identiques résultent de programmations indépendantes.
Un exemple d’erreur possible dans une prévision est donné par l’anti- missile Patriot tiré le 25 février 1991 contre un missile Scud pendant la guerre du Golfe, à Dhahran.
Selon le rapport IMTEC-92-35 de l’US General Accounting Office en date du 4 février 1992, la trajectoire du missile est calculée à partir des indications d’une horloge qui totalise les dizièmes de secondes et les enregistre en mémoire en binaire sur 24 bits, soit 3 octets. Comme 0,1 n’est pas représentable exactement en binaire, le système est amené à tronquer la représentation en introduisant une erreur égale à

soit 0,09536 μs pour chaque pas de 0,1 seconde.
Le missile a été mis en batterie une centaine d’heures avant le déclenchement du tir. Le décalage horaire était donc
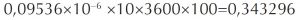
soit 0,34 s. Pendant ce temps le missile Scud évoluant à une vitesse de 1676 m/s a pu parcourir une distance de l’ordre de 600 m.
Le bilan du Scud non intercepté s’est établi à 28 soldats tués.
Remarque : Les bits qui suivent le dernier 0 de la représentation binaire écrite ci-dessus valent 1100100… En remplaçant le dernier bit représenté (0) par un bit 1, l’erreur eut été moindre en temps et donc en distance parcourue par le Scud. Un calcul donne 140 m au lieu de 600 m. Le Scud aurait-il pu être intercepté avec cette troncature suivie d’un arrondi plus judicieux ?
Un autre exemple est celui de la fusée Ariane 5 qui a explosé en vol le 4 juin 1996 à cause d’une erreur de programmation. Citons un extrait du rapport de la commission d’enquête :
L’exception logiciel interne du SRI (Système de Référence Inertielle) s’est produite pendant une conversion de données de représentation flottante 64 bits en valeurs entières 16 bits. Le nombre en représentation flottante qui a été converti avait une valeur qui était supérieure à ce que pouvait exprimer un nombre entier à 16 bits.
Et la commission de suggérer de remplacer l’adage en vigueur :
Un logiciel doit être considéré correct tant qu’il ne s’est pas révélé défaillant.
par celui-ci :
Un logiciel est présumé défaillant tant qu’il n’a pas été jugé correct par les meilleures pratiques en vigueur.
Cet adage peut servir de conclusion à ce paragraphe.
5. CONCLURE ?
Que peut-on conclure de cet inventaire de quelques difficultés liées aux prévisions scientifiquement établies ?
L’opinion et les dirigeants politiques aimeraient disposer de quasi- certitudes pour éviter d’avoir à se réfugier derrière un principe de précaution aux contours bien incertains.
Entre confiance béate et doute systématique et obstiné, on pourra pratiquer le balancement circonspect en se rappelant que :
- établir des prévisions est et restera un exercice difficile, pour des raisons fondamentales liées à la qualité et aux propriétés des modèles ainsi qu’à l’insuffisance éventuelle de données ;
- des prévisions précises existent, faites par des experts appartenant à des organismes publics. Citons à titre d’exemples : la météorologie à court terme, la consommation journalière d’électricité faite par RTE, le trafic routier, etc. ;
- l’énoncé de prévisions devrait être accompagné, au moins dans les cas où ce n’est pas trop technique, des hypothèses retenues pour effectuer les calculs. C’est le cas pour les prévisions – les projections – démographiques, comme on l’a vu ;
- en fonction des hypothèses retenues, les prévisions des experts peuvent être sensiblement différentes. L’amplitude du réchauffement climatique en est un bel exemple ;
- les prévisions formulées par des experts dits indépendants, sans qu’il soit généralement précisé de qui ni de quoi ils sont censés être indépendants, devraient être accueillies avec prudence, voire réserve.
Jacques Burger
~~~~
[1] Institut de Mécanique Céleste et de Calcul des Éphémérides.
[2] www.bourbaphys.fr/laskar.pdf
[3] Voir la référence [2] plus haut.




