Cahier Rationaliste N° 660/661 Mai-août 2019
La vérité en sciences et en mathématique
(première partie)
La notion de vérité est en pratique différente en sciences de la nature et en mathématiques, même si sur le plan philosophique elles relèvent d’une même perception des relations humaines. Il me semble utile de voir en quoi elles diffèrent. Dans une deuxième partie, nous élargirons cette réflexion au cas des probabilités et de la statistique, puis nous verrons quelques perversions de cette vérité.
PRINCIPES DE LA DÉMARCHE SCIENTIFIQUE
Les scientifiques utilisent la raison pour connaître et comprendre la réalité plutôt que de faire appel à d’autres démarches, qu’elles soient mystiques ou métaphysiques. Ils partent du principe que l’univers reste intelligible par la raison humaine. Ils mettent en avant le doute cartésien qui est un des fondements de la démarche scientifique. Ce doute s’est révélé être un puissant moteur de la découverte scientifique. La science admet que toute vérité doit être soumise à des vérifications et peut être remise en cause chaque fois qu’un nouveau fait apparaît. Ainsi, la démarche scientifique procède par le doute raisonnable. La démarche scientifique est aussi basée sur la conviction que le monde observé n’est pas essentiellement trompeur et que des vérités intangibles, voire immuables, existent dans l’univers.
Selon Pierre Crépel[1],
Ne pas confondre « science » et « vérité », même si la science cherche, autant qu’elle le peut, à approcher des vérités (plutôt que des erreurs ou des mensonges). On s’accorde à condamner le « relativisme » qui noierait les sciences dans la sociologie, ou pire, mettrait sur le même plan l’astronomie et l’astrologie. On s’accorde pour reconnaître dans les sciences à la fois une aspiration à la cohérence théorique, mais aussi une inspiration (et une validation) dans l’observation et l’expérience (la déduction et l’induction). Mais doit-on insister sur l’unité de la démarche scientifique au-delà de la diversité évidente, ou au contraire sur la « science plurielle » ? Le matérialisme ne s’oppose pas à l’imagination. La dialectique, et même la pensée du complexe, ne tirent pas un trait définitif sur des conceptions traditionnelles plus simplificatrices voire plus réductrices, qui gardent leur pertinence dans bien des cas.
VÉRIFICATIONS DE NOUVELLES CONNAISSANCES
Pour valider de nouvelles théories, il faut vérifier de façon rigoureuse leur adéquation aux faits expérimentaux. Sinon, pour un scientifique, ce serait une erreur de croire, comme certains philosophes grecs, que la puissance du raisonnement peut éviter tout recours à l’expérience.
Un principe clé de la méthode scientifique est que personne ne peut déclarer exacte une allégation, si elle ne peut la justifier par des preuves expérimentales ou des arguments théoriques. On n’a pas réponse à tout, et des tests empiriques peuvent éviter bien des erreurs. Il faut être méfiant envers des informations tronquées, incomplètes, car elles peuvent nous conduire à des interprétations erronées et à affirmer de complètes inepties.
FALSIFIABILITÉ OU RÉFUTABILITÉ
Depuis l’origine, la philosophie s’est attachée à distinguer le vrai du faux, le juste de l’injuste et à reformuler les problématiques, en élaborant des outils de réflexion destinés à aider les hommes à s’affranchir des limites intellectuelles qui délimitent leur représentation du monde.
Dans son livre Logik der Forschung (Logique de la recherche), publié en 1934, Karl Popper (1902-1994) place le principe de falsification ou de réfutation au cœur de la démarche scientifique : démontrer la fausseté d’une conclusion par l’expérience entraîne la fausseté de la théorie de laquelle elle est déduite[2], en vertu du principe logique qui veut que du faux, on ne peut conclure le vrai. Karl Popper met la Science et sa méthodologie au centre des discussions. Pour lui, il y a un critère de démarcation entre les théories qui se présentent à bon droit comme scientifiques et celles qui relèvent d’une pseudo-science. Ce critère est celui de la réfutabilité ou falsifiabilité qui pourrait assurer le caractère scientifique d’une connaissance.
Selon Thomas Kuhn, c’est à Karl Popper que revient le mérite d’avoir proposé des critères précis permettant :
De distinguer les sciences des pseudo-sciences. Sa formation à la fois philosophique et scientifique, de même que ses engagements humanitaires et sa passion de jeunesse pour la psychanalyse, lui ont permis de comprendre très tôt, que les véritables scientifiques formulent leurs hypothèses de façon à en déduire des faits observables qui pourront les confirmer si elles sont adéquates ou les infirmer si elles ne le sont pas. Il a posé aussi qu’une affirmation dont on ne peut prouver ni qu’elle soit fausse ni qu’elle soit vraie ne peut pas entrer dans les critères de la science. Enfin, la science véritable s’auto-évalue en permanence, le scientifique s’appuie sur des vérités provisoires, de nouvelles expériences peuvent les réfuter et faire émerger de nouveaux paradigmes[3].
Sans être un guide incontestable pour la pensée scientifique, l’apport de Popper pour une approche rationnelle de la notion de vérité en sciences est d’avoir donné comme incontournable la vérification expérimentale de connaissances de nature théorique ou d’observations non corroborées par la construction de modèles permettant la compréhension des phénomènes en jeu, y compris en mathématiques par des expérimentations numériques par exemple.
LA MODÉLISATION : UNE TRANSITION ENTRE OBSERVATION SCIENTIFIQUE ET CONSTRUCTION THÉORIQUE DE LA CONNAISSANCE
Élaboration d’une théorie par un processus de modélisation
La modélisation permet de quantifier un phénomène observé et d’en construire une théorie. La science ne fournit en fait que des modèles de la Réalité s’intégrant au sein de théories. Elle n’a jamais affirmé que ces modèles seraient « la vérité absolue ultime », ou qu’elle détiendrait la Vérité avec un grand V. La science admet seulement que les modèles élaborés et les lois simples qui en sont déduites, ne sont que l’approximation d’une réalité inaccessible dans sa totalité.
D’après John Von Neumann[4] :
Les sciences n’essayent pas d’expliquer ; c’est tout juste si elles tentent d’interpréter ; elles font essentiellement des modèles. Par modèle, on entend une construction mathématique qui, à l’aide de certaines interprétations verbales, décrit les phénomènes observés. La justification d’une telle construction mathématique réside uniquement et précisément dans le fait qu’elle est censée fonctionner.
Ainsi, beaucoup de justifications ou de réfutations d’une connaissance peuvent se faire au moyen de modélisations matérielles ou théoriques.
Modèle concret
Un bel exemple de modèle physique contemporain est celui de la fabrication préalable à Rochefort d’un modèle réduit de l’Hermione. Ce bateau à voiles, lancé en 2014, est une copie à l’identique de la frégate de la fin du XVIIIe siècle qui conduisit le marquis de La Fayette de Rochefort à Boston en 1780. Cette maquette a permis de vérifier, avec quelques mois d’avance, si telle ou telle hypothèse pour la construction du navire était cohérente avec les contraintes géométriques et techniques que son architecture complexe imposait.
Un des cas historiques les plus célèbres furent les expériences sur la datation de la Terre par Georges-Louis Leclerc, comte de Buffon en 1770. Il concevait à juste raison que la Terre avait été jadis une boule de feu qui, peu à peu, s’était refroidie pour donner le globe tiède sur lequel nous vivons. Buffon était un esprit curieux et rationaliste qui sut distraire, du profit espéré de ses forges, la part qu’il fallait pour satisfaire son désir de connaître.
Maître de forges, Buffon fit modeler des boules sphériques de fer de plusieurs tailles définies, les fit chauffer à blanc puis mesura le temps nécessaire pour qu’elles refroidissent à la température de la forge[5]. Il en tira une loi qui reliait le temps de refroidissement de la boule à sa taille. Cette loi, connaissant la taille de la Terre, lui permit de calculer le temps que cette dernière aurait mis pour se refroidir depuis sa formation. Comme la Terre n’est pas du fer, il fit façonner d’autres boules de métaux divers, de marbre et d’argile. Il pratiqua ainsi une multitude d’expériences de physique et d’études de fossiles et autres matériaux. Tout cela pour aboutir au résultat suivant : la Terre aurait plus de 75 000 ans. Cette date était une limite inférieure car la température du Soleil est très supérieure à celle obtenue avec une combustion de tourbe. En fait, selon Gabriel Gohau, Buffon dans son manuscrit, avait conclu à une limite supérieure à 3 millions d’années. Par prudence il a conservé ces 75 000 ans, mais il a dû se rétracter pour ce nombre, car pour l’Église Romaine de l’époque, la date ne pouvait qu’être proche des 5800 ans prévus par la Genèse[6].
La déraisonnable efficacité des mathématiques
Depuis Euclide les mathématiques ont été associées à la pensée logique et rationnelle et ont contribué au développement des sciences, donc des connaissances validées. De nombreuses observations ont apporté la conviction que les lois de l’univers peuvent être décrites par des modèles mathématiques.
Eugène Wigner soulignait la déraisonnable efficacité des mathématiques[7].
Selon Etienne Klein :
L’efficacité d’une théorie mathématique peut aussi venir du fait qu’elle met en évidence des structures « explicatives ». Exemple : les théories de jauge par lesquelles on décrit aujourd’hui l’interaction électrofaible ne manifestent pas seulement leur efficacité par le fait qu’elles reproduisent les données recueillies auprès des détecteurs. Elles sont aussi et surtout efficaces parce qu’elles donnent un schéma expliquant la structure de cette interaction électrofaible en termes de symétries abstraites[8].
MODÈLES MATHÉMATIQUES, ABSTRACTIONS ET CONSTRUCTIONS THÉORIQUES
Théories mathématiques
Les connaissances mathématiques sont par nature théoriques. Elles concernent des propriétés d’objets abstraits comme des nombres, des fonctions, des figures géométriques, des structures algébriques ou topologiques, etc. Ces objets et ces propriétés n’ont de sens qu’au sein de théories, souvent construites pour représenter des parts de réalité décrites par des processus de modélisation.
Les Éléments d’Euclide ont été considérés durant des siècles comme le prototype de telles théories. Par 35 définitions, 6 demandes (ou postulats) et 9 notions communes (axiomes des grandeurs), Euclide fonde une géométrie dont les objets sont des figures idéales (la droite n’a pas d’épaisseur…) et les propriétés sont des relations entre ces objets qu’Euclide appelle propositions[9], dès lors qu’elles sont conséquences des définitions et des demandes selon un raisonnement logique.
Ces méthodes de raisonnements rationnels et les règles de la logique ont fait l’objet de nombreux travaux depuis Eudoxe et Aristote, dont le principal mérite est d’avoir montré dans sa Logique qu’il est possible de réduire tout raisonnement correct à l’application systématique d’un petit nombre de règles.
Déjà au treizième siècle, selon Émile Charles[10], pour Roger Bacon (1264- 1294),
Les mathématiques sont la porte et la clé des sciences et des choses de ce monde et donnent une connaissance certaine de celles-ci. En premier lieu, toutes les catégories dépendent d’une connaissance de la science dont traite les mathématiques et, par conséquent, toute l’excellence de la logique dépend des mathématiques.
LA VÉRITÉ EN MATHÉMATIQUES
Jean Dieudonné, chef de file du groupe Bourbaki, déclarait dans les années 60 : depuis Euclide, qui dit mathématique dit démonstrations. Les mathématiques contemporaines montrent que ce n’est pas si simple (cf. la pensée probabiliste dans la deuxième partie). La vérité en mathématiques dépend en fait des modèles considérés. Un modèle doit avant tout être cohérent, sans contradictions internes. Il doit être aussi utile, c’est-à-dire représenter une réalité concrète sur laquelle il apporte des informations nouvelles. Si les conclusions tirées des résultats du modèle sont conformes aux observations scientifiques de la réalité considérée, on considère alors que ce modèle est assez fiable (provisoirement) pour représenter cette réalité. Sinon, on le jette.
Prenons comme exemple de modèle mathématique la géométrie euclidienne. Elle représente bien notre perception de l’espace environnant. Mais la théorie de la Relativité générale d’Einstein (1915) et ses nombreuses applications concrètes ont montré que la géométrie euclidienne n’est qu’une approximation des propriétés de l’espace, relatives à la finitude de la vitesse de la lumière dans notre univers.
La géométrie euclidienne avait fait l’objet de doutes et de contestations bien avant. Popper dirait de « réfutations ». Il s’agit en fait du cinquième postulat dit postulat des parallèles, dont l’énoncé ressemble à une proposition démontrable (sa réciproque est elle-même démontrable en géométrie absolue, i.e. sans le cinquième postulat).
Euclide l’énonce ainsi :
Si une droite tombant sur deux droites, fait les angles intérieurs et du même côté plus petits que deux droits, les deux droites, infiniment prolongées, se rencontreront du côté où sont les angles plus petits que deux droits.
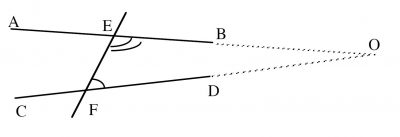
Les lycéens préfèrent cet énoncé équivalent (à partir des quatre autres postulats) dû à John Playfair (début du XIXe siècle), déjà donné au cinquième siècle par Proclus de Lycie (412 – 485) : Par un point extérieur à une droite passe au plus une parallèle à cette droite.
Parmi de très nombreux énoncés équivalents, on a le suivant :
Si les droites d et d’ sont parallèles et si la droite ∂ est perpendiculaire à d, alors ∂ est perpendiculaire à d’.
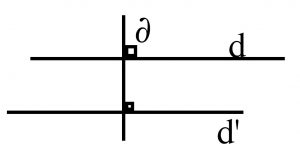
Proclus avait tenté de démontrer ce cinquième postulat. Sa « démonstration » était fausse mais remarquablement bien construite. Le cinquième postulat se cache sous des formes qui semblent être évidentes, comme par exemple de pouvoir déplacer une figure parallèlement à elle-même. Proclus partait de la propriété « évidente » qu’étant données deux droites parallèles, si une droite coupe l’une, elle coupe l’autre. Le développement des géométries non euclidiennes au XIXe siècle montrera un modèle où ce n’est pas vrai.
Omar Al-Khayyâm (1040 – 1131) Commentaires sur les difficultés de certains postulats du Livre d’Euclide[11], partant de l’idée que deux perpendiculaires à une même droite sont équidistantes, construit rigoureusement des quadrilatères égaux (à partir d’un côté de base et des perpendiculaires élevées sur ses extrémités et d’une perpendiculaire à l’une d’elles), empilés, pour s’apercevoir, après une étude très rigoureuse, que les côtés opposés de ces rectangles semblent s’incurver, si l’on n’utilise pas le cinquième postulat pour conclure que le quatrième angle non construit est droit.
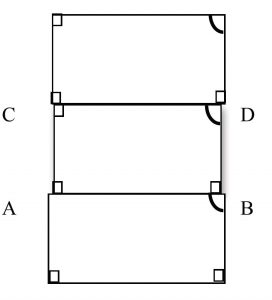
Omar Al-Khayyâm procède en deux étapes :
– Il élimine d’abord l’hypothèse qu’ils sont aigus, car dans ce cas CD > AB et les droites (AC) et (BD) s’écarteraient l’une de l’autre de part et d’autre de [AB];
– ou obtus, car (AC) et (BD) se rapprocheraient l’une de l’autre de part et d’autre de [AB].
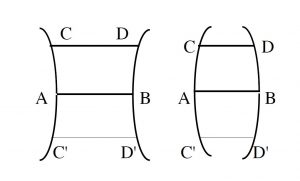
Les perpendiculaires en A et B à [AB] semblent alors cintrées. Il remarque :
On a donc deux lignes droites qui coupent une ligne droite selon deux angles droits, et la distance entre elles augmente ou diminue des deux côtés de cette ligne. C’est là une absurdité première, dès lors que l’on conçoit la linéarité et que l’on réalise la distance entre les deux lignes […] il est donc impossible que les deux lignes [AB] et [CD] soient inégales. Et dès lors qu’elles sont égales, les deux angles seront deux angles droits.
Autrement dit, si les droites sont bien droites, le 5e Postulat est démontré.
L’argument d’Omar Al-Khayyâm relève donc de l’appréhension sensitive et ne s’appuie sur aucune donnée de géométrie théorique. Il met en valeur le sens profond du 5e postulat pour lequel les droites de la géométrie euclidienne sont « bien droites », telles qu’on se les représente intuitivement. En rejetant cette intuition, on ouvre la porte aux géométries non euclidiennes.
Girolamo Saccheri (1667-1733, Italie) : Euclide lavé de toute tache.
Saccheri réfute facilement l’hypothèse que les angles C et D sont obtus (qui aboutit à une géométrie sphérique), mais, comme Omar Al-Khayyâm, il ne peut conclure dans l’hypothèse de l’angle aigu, ne pouvant exclure que deux droites soient asymptotes :

Saccheri ne peut qu’affirmer : L’hypothèse de l’angle aigu est absolument fausse car cela répugne à la nature de la ligne droite.
La configuration du rectangle fut également reprise par : Johann Heinrich Lambert (1728-1777, Suisse : Theorie der Parallellinien).
Lambert montre que l’hypothèse de l’angle obtus est impossible dans une géométrie où les droites sont infinies, mais remarque que cette propriété est vérifiée sur une sphère.
Il pousse l’hypothèse de l’angle aigu le plus loin possible, et obtient les premiers résultats en géométrie hyperbolique (par exemple, l’existence d’une mesure absolue et que la somme des angles d’un triangle ABC dépend de son aire : 2 droits – (a+b+c) = k aire (ABC)
Mais, considérant qu’il n’y a pas de mesure absolue dans l’espace des longueurs en physique et convaincu que les axiomes de la géométrie doivent refléter notre perception de l’espace, il écarte aussi l’hypothèse de l’angle aigu pour obtenir le 5e postulat qu’il n’a donc pas démontré mathématiquement.
Lambert fut traumatisé par ces propriétés non euclidiennes à la fausseté improuvable.
Jean Le Rond D’Alembert (1717-1783), secrétaire de l’Académie royale des sciences, écrira dans la Grande Encyclopédie (v. 1765) : La définition et les propriétés de la ligne droite, ainsi que des lignes parallèles sont l’écueil et pour ainsi dire le scandale des Éléments de géométrie.
Il fallait oser transgresser l’intuition. Bolyaï, Lobatchevski et Gauss l’ont fait. Carl Friedrich Gauss (1777-1855), après 30 ans de recherches, écrit en 1817, cet aveu prémonitoire : Je suis de plus en plus convaincu que la nécessité de notre géométrie euclidienne ne peut être prouvée en tout cas par une pensée humaine et pour une raison humaine. Peut-être dans une autre vie il nous sera possible d’avoir une indication sur la nature de l’espace qui nous est pour le moment inaccessible.
Ainsi le modèle euclidien s’est avéré robuste jusqu’à l’invention des géométries non euclidiennes qui ne représentent pas notre espace environnant. Il est encore utilisé comme approximation à notre échelle de la géométrie de la Relativité générale.
Einstein avait donné son point de vue devant l’Académie des sciences de Berlin en 1921 : La géométrie pratique est une science dérivée de l’expérience, nous la distinguons de la géométrie axiomatique. La question de savoir si la géométrie pratique du monde est euclidienne ou non, a un sens précis et la réponse ne peut être fournie que par l’expérience.
EXPÉRIMENTATIONS NUMÉRIQUES ET CONJECTURES
Avec les nouveaux outils de calcul, le numérique automatisé a pris sa place dans les démonstrations mathématiques. L’exemple prototypique est le théorème des quatre couleurs (comment colorier une carte de géographie avec seulement 4 couleurs, sans qu’il y ait de frontière commune entre deux zones de même couleur). Le théorème affirme que c’est possible quelle que soit la carte donnée. Mais sa démonstration suppose des calculs tellement nombreux que les humains en sont incapables. Un ordinateur effectuant des milliards d’opérations par seconde donne la réponse. Les mathématiciens donnent le théorème comme démontré et vrai, mais les puristes contestent que l’usage d’un instrument de calcul déroge à la pratique ancestrale de la démonstration.
Mais il y des énoncés qui semblent vrais mais dont on n’a pas encore démontré leur véracité. On appelle cela une conjecture. Lors du deuxième congrès international des mathématiciens, tenu à Paris en août 1900, David Hilbert présenta une liste de problèmes qui tenaient jusqu’alors les mathématiciens en échec. Ces problèmes devaient, selon Hilbert, marquer le cours des mathématiques du XXe, et l’on peut dire aujourd’hui que cela a été grandement le cas. Publiée après la tenue du congrès, la liste définitive comprenait 23 problèmes, aujourd’hui appelés les problèmes de Hilbert. Treize d’entre eux ont été résolus et ne sont donc plus des conjectures.
Parmi les conjectures célèbres, la plus simple à énoncer est la conjecture de Christian Goldbach (1742)[12] : tout nombre entier pair supérieur à 3 peut s’écrire comme la somme de deux nombres premiers.
C’est l’un des plus vieux problèmes non résolus de la théorie des nombres et des mathématiques. Il partage avec l’hypothèse de Riemann et la conjecture des nombres premiers jumeaux le numéro 8 des problèmes de Hilbert, énoncés par celui-ci en 1900.
Cette conjecture a fait l’objet de nombreux travaux. De 1920 à 2013, on peut citer au moins dix-sept publications majeures sur ce problème. La majorité des mathématiciens pense que la conjecture de Goldbach est vraie, en se basant surtout sur des considérations statistiques axées sur la répartition des nombres premiers : plus le nombre est grand, plus il y a de manières disponibles pour le représenter sous forme de somme de deux ou trois autres nombres. Les vérifications numériques sur ordinateur ont montré que la conjecture de Goldbach est vérifiée pour tous les entiers pairs jusqu’à 4·1018 (Tomás Oliveira e Silva, Siegfried Herzog et Silvio Pardi)[13]. Peut-on direqu’elle est vraie ?
QUELLE VÉRITÉ EN STATISTIQUE ET EN PROBABILITÉS ?
Dans une deuxième partie nous verrons que ces remarques sur la question de la vérité en mathématiques telles que nous les avons développées, s’avèrent inadaptées dans un contexte probabiliste, et notamment insuffisantes dans le contexte de la statistique inférentielle, quand toute affirmation est entachée d’une probabilité de ne pas se tromper. Le « calcul des probabilités », inventé au XVIIe siècle dans une correspondance entre Blaise Pascal et Pierre de Fermat, a été considéré jusqu’au XXe siècle comme une application directe des mathématiques aux situations où le hasard intervient et donc impropres à des prévisions rigoureuses. La plupart des évaluations découlaient de la formule de Laplace : nombre des cas favorables / nombre des cas possibles, quand on peut considérer que tous les cas sont équiprobables[14]. Devant ces fondements peu assurés, Andreï Kolmogorov a fondé en 1933 une théorie axiomatique dans son article : Fondements de la théorie des probabilités. Le « modèle probabiliste » ainsi dégagé permet aujourd’hui de grandes avancées dans tous les domaines des connaissances quand la relation de cause à effet, intrinsèque à toute connaissance scientifique, est de nature aléatoire.
Michel Henry
~~~~
- Crépel, Pierre (2018), Les sciences, leur histoire, leur enseignement. Carnets rouges n°14, octobre 2018, col. Sciences et éducation, réseau-école.pcf.fr.
- Karl-Raimund Popper, Logique de la découverte scientifique, titre dérivé de la traduction en anglais : The Logic of Scientific Discovery, éd. Flammarion Paris, 1973, p. 74, 75.
- Thomas Kuhn, La structure des révolutions scientifiques, Flammarion, 1972.
- Cité par James Gleick, La théorie du chaos, éditions Albin Michel, Paris, 1989.
- Buffon fit ces expériences dans ses forges du village de Buffon à côté de Montbard.
- Buffon, Des époques de la nature, introduction et notes de Gabriel Gohau, p. xxII, première époque 58 et seconde époque, p. 65, Nouvelles éditions rationalistes, coll. « Lumières de tous les temps, 1971.
- E. P. Wigner, The Unreasonable Effectiveness of Mathematics in the Natural Sciences, in Communications on Pure and Applied Mathematics. XIII (1960).
- Etienne Klein, L’efficacité des mathématiques est-elle si « déraisonnable » ? Forum de la théorie, 6-7 décembre 2005, Paris.
- Certaines ont été par la suite érigées en théorèmes, comme celui de Pythagore, ainsi dénommé par Proclus au 5e siècle.
- Émile Charles, Roger Bacon, sa vie ses ouvrages et ses doctrines, librairie Hachette, Paris 1861, livre V.
- Roshdi Rashed, Histoire des sciences arabes, Paris, Seuil, 1997.
- Le 7 juin 1742, le mathématicien prussien Christian Goldbach écrit au mathématicien suisse Leonhard Euler une lettre à la fin de laquelle il propose sa conjecture. Dans sa réponse datée du 30 juin 1742, Euler rappelle à Goldbach que cet énoncé découle d’un énoncé antérieur que Goldbach lui avait déjà communiqué.
- Pour le plaisir, on pourra lire cet excellent ouvrage de Apostolos Doxiadis: Oncle Petros et la conjecture de Goldbach, Points poche
- C’est un cercle vicieux de définir la notion de probabilité en l’utilisant comme déjà là.




